1. 머신러닝과 선형대수학의 연관성
선형대수학을 왜 배워야 하는 것일까?
먼저 머신러닝을 정의할 필요가 있다.
머신러닝 : "주어진 데이터를 분석하고 학습한 후, 새로운 결정을 내릴때 학습한 내용을 적용하는 알고리즘"
데이터를 분석 학습하는 과정은 함수(function)에 집어 넣어 처리한다.
이 함수, 연립방정식의 해를 구하는 방법을 연구한 학문이 선형대수학이다.
예를 들어 3개의 연립 방정식이 아래와 같이 주어졌을 때
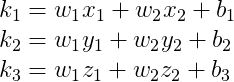
위의 연립 방정식을 행렬 수식를 이용해서 표현해보면 아래와 같이 나눌 수 있다.



위의 세 행렬 수식을 통해서 아래의 하나의 수식을 만들어 낼 수 있다.

복잡하고 다양한 데이터들을 수집해서 행렬화 한 후, 함수(function)에 집어 넣어 처리하는 과정은
선형대수학의 해를 구하는 것과 같다.
즉 데이터를 내가 원하는 형태로 가공하는 알고리즘을 짜기 위해서는,
선형대수학에 대한 기초적인 이해가 있어야 한다는 것이다.
reference
선형대수가 왜 머신러닝에 있어서 가장 중요한 수학인가?
머신러닝과 선형대수의 관계
medium.com
머신러닝 기초 - 선형 대수 - 머신러닝
머신러닝을 학습할 때, 왜 선형대수학을 배워야할까요? 컴퓨터가 "배운다"는 행위를 하기 위해서는, 엄청난 양의 데이터를 받아들여, 처리할 줄 알아야 합니다. 데이터를 처리한다는 것은 정말
opentutorials.org
2. 선형대수학 기초용어 정리(Scalar,Vector, Matrix, Dimension)

위에 예시를 든 연립방정식은 아래와 같은 행렬로 나타낼 수 있다.

그리고 이 행렬은 아래의 수식으로 간단하게 나타낼 수 있다.

이 수식을 기초로 Scalar,Vector, Matrix, Dimension 의 정말 기초적인 기본 개념을 생각해보자
- 스칼라(Scalar)는 하나의 상수 즉 숫자를 의미한다.
위의 수식 y = A*x 에서 A 앞에 생략되어 있는 1이 이에 해당된다.
만약 A가 매트릭스(Matrix)가 아니고 상수 A = 3 일 경우, A는 스칼라가 된다.

- 벡터(Vector)는 순서가 있는 행렬, 또는 배열(array)를 의미한다.

- 매트릭스(Matrix)는 가로(row)와 세로(column) 두개의 축을 가진 2차원 행렬이다. 이는 백터의
매트릭스 안에는 y = A*x에서 "y와 x의 관계"에 대한 정보를 담고 있다.

- 차원(Dimension)은 매트릭스의 행과 열의 숫자를 낸다. 즉 A는 m x n 차원의 매트릭스이다.